

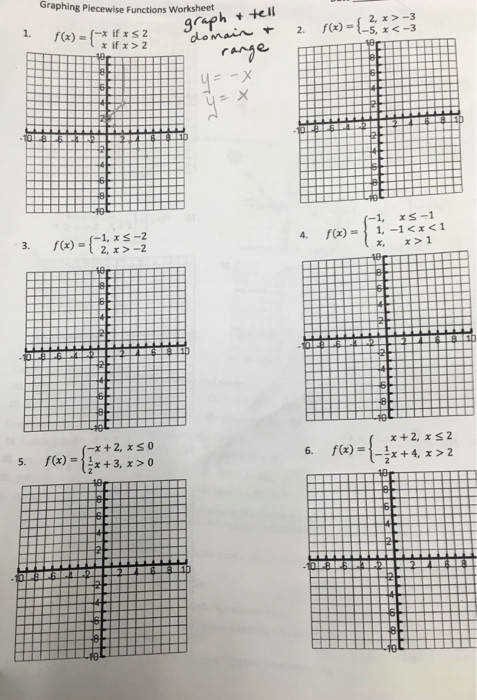
A closed circle indicates that the point is included in the interval The absolute value function is a very good example of a piecewise function. The graph of a piecewise function has different pieces corresponding to each of its definitions. An open circle indicates that the point is not included in the interval A piecewise function is a function f (x) which has different definitions in different intervals of x. Example Suppose that a battery provides no voltage to a circuit when a switch is open. Intervals: To denote the edges of the loops, we are using the same notation as for the intervals of the solutions of the inequalities, remember? Piecewise functions are a favorite of engineers. As another example, let’s take f (x) x 2, this function behaves in the same way for all the values in. It can be represented in mathematical form as f (x) 3. For example: If a function takes on any input and gives the output as 3. As the name implies, these functions are defined by chunks of functions for each part of the domain. A function is a mathematical object which associates each input with exactly one output. As you move each slider, constants and coefficients in the functions are changed, and thus the graphs of each function move to satisfy the new parameters. Piecewise functions are functions that are defined by different formulas or functions for each interval. Doing so is common in mathematics, but especially when typing piecewise functions and systems of equations/inequalities. The absolute value function is a very good example of a piecewise function. Piecewise functions and equation alignment Here well see some of MathType capabilities for controlling alignment of multiple lines.
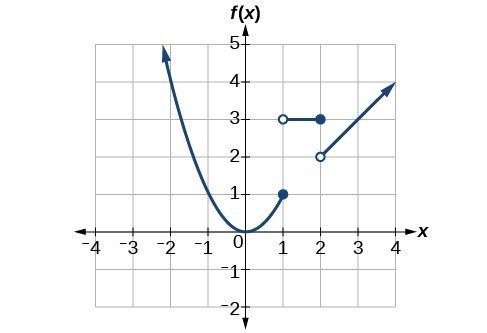
The following GeoGebra lab features several rational functions whose domains are defined by sliders. A piecewise function is a function f(x) which has different definitions in different intervals of x. Lesson Objective: This interactive lesson to help students understand of piecewise-defined functions.ĭefinition: A piecewise function is a function that consists of two or more standard functions defined on different domains.


 0 kommentar(er)
0 kommentar(er)
